|
SAT SUMX = 5846, SUMX^2 = 3428148
A)
Mean = 5846 / 10 = 584.6
B) S = ((SUMX^2-(((SUMX)^2)/N))/(N-1))^.5
S =
((3428148-(((5846)^2)/10))/(10-1))^.5
S = ((3428148-3417571.6)/9)^.5
S = 1175.12^.5
S = 34.28
C) 95%CI = +- t(.05)SsubXBAR + XBAR
SSubXBAR = (s)/(n^.5) = 34.28/3.16 = 10.85
95%CI = +- t(.05)10.85 + 584.6 = +-(2.2622*10.85)+ 584.6
95%CI = 560.07 - 609.13 or the
whole scores of 560-609. 542 is not in the expected range of the population mean, thus the
course has a statistical significance of improving the
scores.
By using a confidence interval of 95%, we can be 95% sure
that the population mean is contained within 560.06 -
609.14. Since a mean of 542 is not within this range, we
have can conclude that the new course did indeed improve the
SAT verbal scores.
By performing a one-tailed t test we can analyze this:
Set H0: u0<=u
Set H1: u>u0
in plain language: our null hypothesis is that the sample
mean is equal to or less than the population mean. Our
alternative hypothesis is that the sample mean is greater
than the population mean.
 t
= (584.6-542)/(10.841) = 3.93 t
= (584.6-542)/(10.841) = 3.93
t(.01),df=9 = 2.82, p<.01
Rejection Rule: For H1:m >
m0,
reject H0
if tcomp >
tcrit
We reject H0.
The new course did improved the SAT verbal scores
Question #2
Descriptive
Statistics
|
|
N |
Mean |
Std. Deviation |
Variance |
|
Yellow |
5 |
20.6000 |
4.39318 |
19.300 |
|
Green |
4 |
29.2500 |
12.09339 |
146.250 |
|
Valid N (listwise) |
4 |
|
|
|
Our Null hypothesis: H0 = u1 - u2 = 0 (there is no
difference in the scores of the yellow group and green
group)
Our alpha level is .05, we are looking for a 95% CI
Since N is different for each group, we use the formula:
s sub Xbar sub 1 minus X bar sub 2 = ((((N1-1)(s2sub1) +
(N2-1)(S2sub2))/(N1+N2-2))((1/N1)+(1/N2)))^.5
OR: (s2pooled(1/N1 + 1/N2))^.5
S2sub1 = 19.3
S2sub2 = 146.25
N1=5
N2=4
So we get: s2pooled = ((4*19.3)+(3*146.25))/7
s2pooled = 515.95/7 = 73.71
s sub Xbar sub 1 minus X bar sub 2 = (73.71(1/5 + 1/4))^.5 =
5.76, or the standard error difference
Now find t sub xbar sub 1 minus xbar sub 2 = (Xbar1 -
Xbar2)/s sub Xbar sub 1 minus X bar sub 2
=20.60-29.25/5.76 = -1.50
Using table B, we find a critical value for T where df =
N1+N2-2, or 7
Using the 5% level for t(.05) we get 2.36
Rejection Rule: Reject H0 if |tcomp| >= tcrit
|tcomp| = 1.5 which is less than 2.36, or tcrit,
therefore we do not reject H0, meaning that we cannot
conclude the yellow paper caused subjects to score lower.
The answer is no
T-Test, Question 2
Group
Statistics
|
|
Color |
N |
Mean |
Std. Deviation |
Std. Error Mean |
|
Value |
Yellow |
5 |
20.6000 |
4.39318 |
1.96469 |
Green |
4 |
29.2500 |
12.09339 |
6.04669 |
Independent Samples Test
|
|
Levene's Test for Equality of Variances |
t-test for Equality of Means |
F |
Sig. |
t |
df |
Sig. (2-tailed) |
Mean Difference |
Std. Error Difference |
95% Confidence Interval of the Difference |
Lower |
Upper |
|
Value |
3.385 |
.108 |
-1.502 |
7 |
.177 |
-8.65000 |
5.75919 |
-22.26831 |
4.96831 |
Equal variances assumed
Question #3 Statistics
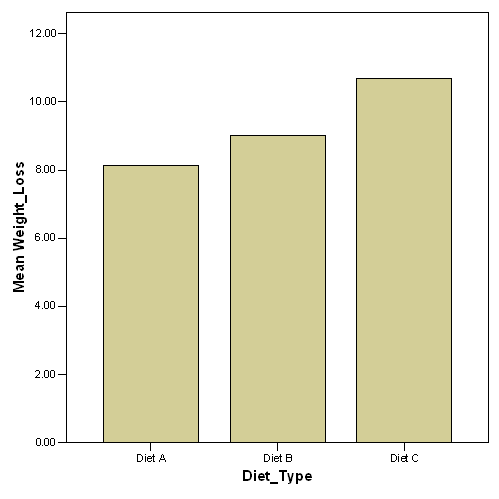
|
|
DietA |
DietB |
DietC |
|
N |
|
8 |
10 |
10 |
|
Mean |
8.1250 |
9.0000 |
10.7000 |
|
Median |
8.0000 |
9.0000 |
11.0000 |
|
Mode |
7.00(a) |
9.00 |
7.00(a) |
|
Std. Deviation |
2.35660 |
2.30940 |
2.75076 |
|
Variance |
5.554 |
5.333 |
7.567 |
| |
|
|
|
|
a
Multiple modes exist. The smallest value is shown
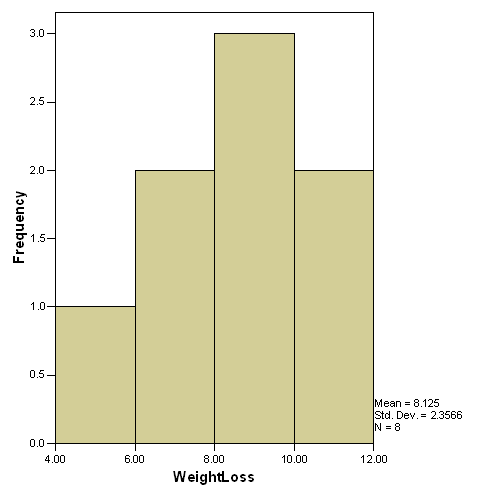
For Diet A, the most appropriate descriptive statistic is the
mean. Since multiple modes exist, the mode is not very useful.
The median is slightly lower than the mean, giving it a slight
positive skew, hence the mean is the most useful.
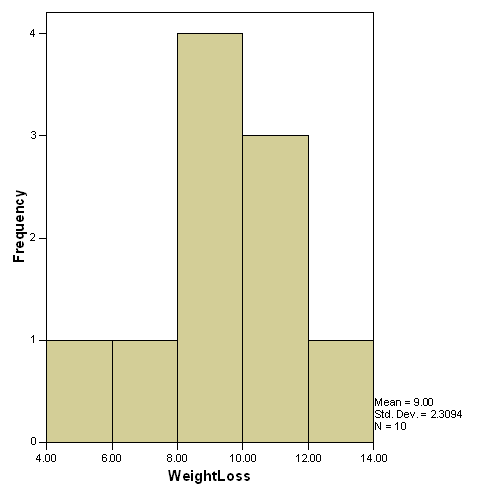
For Diet B, the median, mean and mode are all equal, hence all
useful.
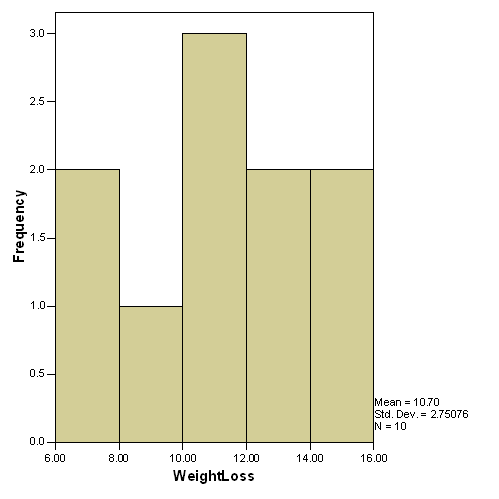
For Diet C, there is a slight negative skew. Multiple modes
exist, so the mode is not useful. Because the skew is only
slight, the mean is the most useful.
Histograms are the best graphs for these diets.
Graph of Diet A
Diet B
Diet C
#3, Oneway ANOVA
Build a matrix of values based on the data for Diet A, Diet B,
Diet C
Ho:
m1 =
m2 =
m3
Ha: At least
one mean differs from the others.
Rejection
Rule: Reject Ho if p-value < .05
 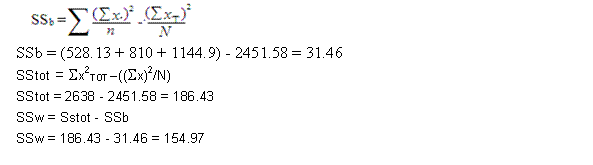  SPSS ANOVA
SPSS ANOVA
Weight_Loss
|
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Between Groups |
31.454 |
2 |
15.727 |
2.537 |
.099 |
|
Within Groups |
154.975 |
25 |
6.199 |
|
|
|
Total |
186.429 |
27 |
|
|
|
P value = .099 > .05 --> Accept H0.
F(2,25) = 3.39 , p = .099
There is no significant difference in mean wieght loss among the
different diets
#3
b) Post Hoc Tests
Multiple Comparisons
Dependent Variable: Weight_Loss
LSD
|
(I) Diet_Type |
(J) Diet_Type |
Mean Difference (I-J) |
Std. Error |
Sig. |
95% Confidence Interval |
Lower Bound |
Upper Bound |
|
Diet A |
Diet B |
-.87500 |
1.18101 |
.466 |
-3.3073 |
1.5573 |
Diet C |
-2.57500(*) |
1.18101 |
.039 |
-5.0073 |
-.1427 |
|
Diet B |
Diet A |
.87500 |
1.18101 |
.466 |
-1.5573 |
3.3073 |
Diet C |
-1.70000 |
1.11346 |
.139 |
-3.9932 |
.5932 |
|
Diet
C |
Diet
A |
2.57500(*) |
1.18101 |
.039 |
.1427 |
5.0073 |
Diet
B |
1.70000 |
1.11346 |
.139 |
-.5932 |
3.9932 |
* The mean
difference is significant at the .05 level.
There was a significant difference between Diet A and Diet C
#3 b) A
graph of the means
#4, Two Way
ANOVA, Type I Sum of Squares
|
|
A |
B |
C |
|
|
M |
Sx11 |
28 |
Sx12 |
57 |
Sx13 |
38 |
SA1 |
123 |
|
Sx211 |
210 |
Sx212 |
547 |
Sx213 |
490 |
SA21 |
1247 |
|
|
7 |
|
9.5 |

|
12.667 |
|
9.462 |
|
n11 |
4 |
n12 |
6 |
n13 |
3 |
nA1 |
13 |
|
F |
Sx21 |
37 |
Sx22 |
28 |
Sx23 |
76 |
SA2 |
141 |
|
Sx221 |
357 |
Sx222 |
206 |
Sx223 |
870 |
SA22 |
1433 |
|
|
9.25 |

|
7 |

|
10.857 |

|
9.4 |
|
n21 |
4 |
n22 |
4 |
n23 |
7 |
nA2 |
15 |
|
|
SB1 |
65 |
SB2 |
85 |
SB3 |
114 |
SXT |
264 |
|
SB21 |
567 |
SB22 |
753 |
SB23 |
1360 |
SX2T |
2680 |
|
|
8.125 |
|
8.5 |
|
11.4 |
|
9.429 |
|
nB1 |
8 |
nB2 |
10 |
nB3 |
10 |
N |
28 |
|
|
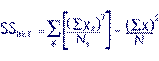
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SSbet =
(28^2/4)+(57^2/6)+(38^2/3)+(37^2/4)+(28^2/4)+(76^2/7)-(264^2/28) |
|
|
=
196+541.5+481.333+342.25+196+825.143-2489.143 = 93.083 |
|
|
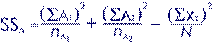
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SSa =
(123^2/13)+(141^2/15)-(264^2/28) |
|
|
|
|
=
1163.769+1325.4 - 2489.143 = 0.026 |
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
(65^2/8)+(85^2/10)+(114^2/10)-(264^2/28) |
|
|
|
=
528.125+722.5+1299.6-2489.143 = 61.082 |
|
|
|
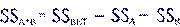
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SSa*b =
93.083-0.026-61.082 = 31.975 |
|
|
|
|
|
|
|
|
|
|
|
|
|
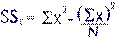
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SSt = 2680 -
(264^2)/28 = 2680 - 2489.14285714286 = 190.857 |
|
|
|
|
|
|
|
|
|
|
|
SSw = SSt -
SSbet |
|
|
|
|
|
|
= 190.857 -
93.083 = 97.774 |
|
|
|
|
|
dfbet = K - 1 =
5 |
K = total
number of groups |
|
|
dfa = A - 1 = 1 |
A = #of cells
in A |
|
|
|
|
dfb = B - 1 = 2 |
B = #of cells
in B |
|
|
|
|
dft = N - 1 =
28-1 = 27 |
|
|
|
|
|
|
dfa*b = 1*2 = 2 |
|
|
|
|
|
|
MSbet =
SSbet/dfbet = 93.083/5 = 18.617 |
|
|
|
MSa = SSa/dfa =
0.026/1 = 0.026 |
|
|
|
|
MSb = SSb/dfb =
61.082/2 = 30.541 |
|
|
|
|
MSa*b =
Ssa*b/dfa*b = 31.975/2 = 15.988 |
|
|
|
MSw = SSw/dfw =
97.774/22 = 4.444 |
|
|
|
|
Fa = MSa/MSw =
0.026/4.444 = 0.006 (df=1,22) |
|
|
|
Fb = MSb/MSw =
30.541/4.444 = 6.872 (df=2,22) |
|
|
Fa*b =
Msa*b/MSw = 15.988/ = 3.598 (df=2,22) |
|
|
|
|
|
|
|
|
|
|
|
Two-Way ANOVA
Summary Table |
|
|
|
|
|
|
Source |
SS |
df |
MS |
F |
|
p |
|
|
Between Groups
(Cells) |
93.08 |
5 |
18.62 |
|
|
|
|
|
A |
|
|
0.026 |
1 |
0.026 |
0.006 (df=1,22) |
|
F(1,22)=0.006,
p>.05 |
|
B |
|
|
61.08 |
2 |
30.54 |
6.872 (df=2,22) |
|
F(2,22)=6.872,
p<.01 |
|
A x B |
|
|
31.98 |
2 |
15.99 |
3.598 (df=2,22) |
|
F(2,22)=3.598,
p<.05 |
|
Within Groups |
97.77 |
22 |
4.444 |
|
|
|
|
|
Total |
|
|
190.9 |
27 |
|
|
|
|
|
F(1,22)=0.006, p>.05
There is no significant population mean difference among Gender
F(2,22)=6.872, p<.01
There is a significant population mean difference in the diets
F(2,22)=3.598, p<.05
There is a significant interaction between diets and gender
Tests of
Between-Subjects Effects
Dependent Variable:
Weight_Loss
|
Source |
Type I Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Corrected
Model |
93.083(a) |
5 |
18.617 |
4.189 |
.008 |
|
Intercept |
2489.143 |
1 |
2489.143 |
560.080 |
.000 |
|
Gender |
.026 |
1 |
.026 |
.006 |
.939 |
|
Diet |
65.377 |
2 |
32.689 |
7.355 |
.004 |
|
Gender *
Diet |
27.680 |
2 |
13.840 |
3.114 |
.064 |
|
Error |
97.774 |
22 |
4.444 |
|
|
|
Total |
2680.000 |
28 |
|
|
|
|
Corrected
Total |
190.857 |
27 |
|
|
|
a R Squared = .488
(Adjusted R Squared = .371)
Because problem #4 contains
different values of n for each group, the Type III sum of squares as computed in
SPSS does not match the manual sweep-matrix as taught in class. So I used a
Type I sum of squares (highlighted) which more closely resembles the manual
calculations.
I am including the
TYPE III SPSS mean of squares results for this question below, with different
answers due to the different results of the same data, neither of which
matches manual computations:
Tests of
Between-Subjects Effects
Dependent Variable:
Weight_Loss
|
Source |
Type III Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Corrected
Model |
93.083(a) |
5 |
18.617 |
4.189 |
.008 |
|
Intercept |
2273.558 |
1 |
2273.558 |
511.571 |
.000 |
|
Gender |
3.045 |
1 |
3.045 |
.685 |
.417 |
|
Diet |
72.486 |
2 |
36.243 |
8.155 |
.002 |
|
Gender *
Diet |
27.680 |
2 |
13.840 |
3.114 |
.064 |
|
Error |
97.774 |
22 |
4.444 |
|
|
|
Total |
2680.000 |
28 |
|
|
|
|
Corrected
Total |
190.857 |
27 |
|
|
|
a R Squared = .488
(Adjusted R Squared = .371)
F(1,22)=0.685, p>.05
There is no significant population mean difference among Gender
F(2,22)=8.155, p<.01
There is a significant population mean difference in the diets
F(2,22)=3.114, p>.05
There is no significant interaction between diets and gender
LSD TEST, POST HOC
Pairwise Comparisons
Dependent Variable:
Weight_Loss
|
(I) Gender |
(J) Gender |
Mean Difference (I-J) |
Std. Error |
Sig.(a) |
95% Confidence Interval for Difference(a) |
Lower Bound |
Upper Bound |
|
Male |
Female |
.687 |
.829 |
.417 |
-1.033 |
2.406 |
|
Female |
Male |
-.687 |
.829 |
.417 |
-2.406 |
1.033 |
Based on estimated
marginal means
a Adjustment for
multiple comparisons: Least Significant Difference (equivalent to no
adjustments).
There is no significant mean difference between Gender
Pairwise
Comparisons
Dependent Variable:
Weight_Loss
|
(I) Diet |
(J) Diet |
Mean Difference (I-J) |
Std. Error |
Sig.(a) |
95% Confidence Interval for Difference(a) |
Lower Bound |
Upper Bound |
|
Diet_A |
Diet_B |
-.125 |
1.009 |
.903 |
-2.218 |
1.968 |
Diet_C |
-3.637(*) |
1.041 |
.002 |
-5.797 |
-1.477 |
|
Diet_B |
Diet_A |
.125 |
1.009 |
.903 |
-1.968 |
2.218 |
Diet_C |
-3.512(*) |
.996 |
.002 |
-5.577 |
-1.446 |
|
Diet_C |
Diet_A |
3.637(*) |
1.041 |
.002 |
1.477 |
5.797 |
Diet_B |
3.512(*) |
.996 |
.002 |
1.446 |
5.577 |
Based on estimated
marginal means
* The mean
difference is significant at the .05 level.
a Adjustment for
multiple comparisons: Least Significant Difference (equivalent to no
adjustments).
There is no
significant difference between Diet A and Diet B
There is a
significant difference between Diet A and Diet C
There is a
significant difference between Diet C and Diet B
|
Two-Way ANOVA Summary Table |
|
|
|
|
|
|
Source |
SS |
df |
MS |
F |
|
p |
|
|
Between Groups (Cells) |
456.8 |
1 |
456.8 |
|
|
|
|
|
A |
|
|
311.1 |
1 |
311.1 |
34.541 (df=1,10) |
|
F(1,10)=34.541, p<.01 |
|
B |
|
|
73.14 |
1 |
73.14 |
8.12 (df=1,10) |
|
F(1,10)=8.12, p<.05 |
|
A x
B |
|
|
72.49 |
1 |
72.49 |
8.047 (df=1,10) |
|
F(1,10)=8.047, p<.05 |
|
Within Groups |
90.08 |
10 |
9.008 |
|
|
|
|
|
Total |
|
|
546.9 |
13 |
|
|
|
|
|
Dependent Variable:
Time
|
Source |
Type I Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Corrected
Model |
456.774(a) |
3 |
152.258 |
16.902 |
.000 |
|
Intercept |
2263.143 |
1 |
2263.143 |
251.228 |
.000 |
|
Gender |
73.143 |
1 |
73.143 |
8.119 |
.017 |
|
Dress |
275.149 |
1 |
275.149 |
30.544 |
.000 |
|
Gender *
Dress |
108.482 |
1 |
108.482 |
12.042 |
.006 |
|
Error |
90.083 |
10 |
9.008 |
|
|
|
Total |
2810.000 |
14 |
|
|
|
|
Corrected
Total |
546.857 |
13 |
|
|
|
a R Squared = .835
(Adjusted R Squared = .786)
|